5.27 ユニタリー行列
定義 5.78 (ユニタリー行列)
行列
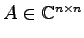 が
が 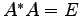 をみたすとき,
をみたすとき,
 をユニタリー行列(unitary matrix)という.
をユニタリー行列(unitary matrix)という.
注意 5.79 (ユニタリー行列と直交行列)
ユニタリー行列  の要素が実数のみであるとき,
の要素が実数のみであるとき,
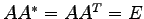 よりユニタリー行列は直交行列となる.
よりユニタリー行列は直交行列となる.
定理 5.80 (ユニタリー行列の性質)
 をユニタリー行列とする.次が成り立つ.
をユニタリー行列とする.次が成り立つ.
- (1).
-
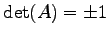 .
.
- (2).
 は正則である.
は正則である.
- (3).
-
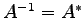 .
.
定理 5.81 (ユニタリー行列と正規直交系)
行列
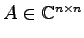 がユニタリー行列であることと,
がユニタリー行列であることと,
 の列ベクトルまたは行ベクトルが
正規直交系であることとは,
必要十分条件である.
ただし,内積は
の列ベクトルまたは行ベクトルが
正規直交系であることとは,
必要十分条件である.
ただし,内積は
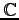 上の内積を用いる.
上の内積を用いる.
問 5.82 (ユニタリー行列と正規直交系)
直交行列の場合と同様に示せ.
問 5.83 (ユニタリー行列の具体例)
次の行列がユニタリー行列となることを示せ.
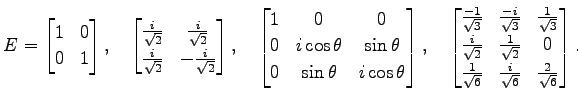 |
平成20年2月2日