2.19 三角関数
単位円(半径 ![]() で中心が原点
で中心が原点 ![]() にある円)
にある円)![]() と
原点
と
原点 ![]() を通る直線
を通る直線 ![]() を用意する.
円
を用意する.
円 ![]() と直線
と直線 ![]() の交点を
の交点を ![]() とする.
点
とする.
点 ![]() より
より ![]() 軸に下ろした垂線と
軸に下ろした垂線と ![]() 軸との交点を
軸との交点を ![]() とする.
点
とする.
点 ![]() を
を ![]() とし,
とし,
![]() を通り
を通り ![]() 軸に平行な直線と直線
軸に平行な直線と直線 ![]() との交点を
との交点を ![]() とする.
とする.
![]() から点
から点 ![]() への円弧の(方向付き)長さを
への円弧の(方向付き)長さを ![]() とする.
このとき,
点
とする.
このとき,
点 ![]() の座標を
の座標を
![]() と定義し,
点
と定義し,
点 ![]() の座標を
の座標を
![]() と定義する.
この定義により得られる関数を
三角関数(trigonometric function)と呼ぶ.
読み方は
と定義する.
この定義により得られる関数を
三角関数(trigonometric function)と呼ぶ.
読み方は ![]() ,
, ![]() ,
, ![]() の順に sine,
cosine, tangent である.
の順に sine,
cosine, tangent である.
三角関数のべき乗
![]() は
は ![]() のように略記する.
しかし
のように略記する.
しかし ![]() のときはこの表記は用いない.
のときはこの表記は用いない.
![]() は逆三角関数を意味する.
このとき表記は
は逆三角関数を意味する.
このとき表記は
![]() や
や ![]() とするか
新たな記号
とするか
新たな記号
 |
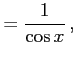 |
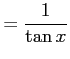 |
を用いる.
定理 2.48 (三角関数は単位円上の点)
 なので
なので
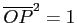 より
導出される.
より
導出される.
(証明) 単位円の半径の長さは
定理 2.49 (三角関数の偶奇)
 ,
, 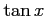 は奇関数であり,
は奇関数であり,
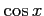 は偶関数である.
は偶関数である.
定理 2.50 (三角関数の周期性)
 ,
, 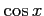 は周期
は周期 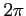 の周期関数であり,
の周期関数であり,
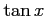 は周期
は周期 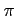 の周期関数である.
の周期関数である.
定理 2.51 (三角関数の加法公式)
三角関数の加法公式:
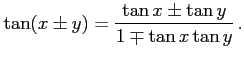 |
定理 2.52 (三角関数の性質)
三角関数どうしの互いの関係:
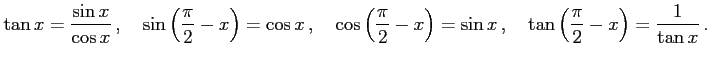 |
問 2.53 (三角関数の性質)
これを示せ.
(答え) 加法公式から導出される.
定理 2.54 (三角関数の合成)
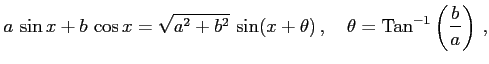 |
|
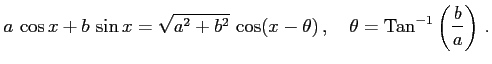 |
問 2.55 (三角関数の合成)
これを示せ.
(答え) 加法公式から導出される.
問 2.56 (三角関数のグラフ)
三角関数の概形を書け.
例 2.57 (三角関数の値)
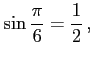 |
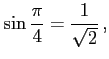 |
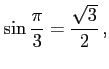 |
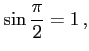 |
|||||||||||
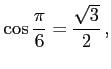 |
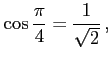 |
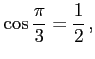 |
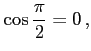 |
|||||||||||
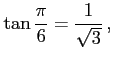 |
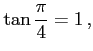 |
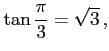 |
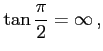 |
問 2.58 ( 倍角の公式)
倍角の公式)
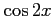 ,
, 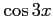 ,
, 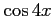 ,
,  を
を
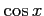 の多項式で表せ.
の多項式で表せ.
(答え)
平成22年6月17日