2 関数

次: 2.1 写像上: 解析学I 前: 1.8 絶対値

2 関数

本章の目次

2.1 写像
2.2 写像の分類
2.3 合成写像
2.4 恒等写像
2.5 逆写像
2.6 関数
2.7 逆関数
2.8 多価関数
2.9 関数のかたち
2.10 関数の上限，下限，最大値，最小値
2.11 初等関数
2.12 一次関数
2.13 べき関数
2.14 多項式関数
2.15 有理式関数
2.16 指数関数
2.17 対数関数
2.18 角度
2.19 三角関数
2.20 逆三角関数
2.21 双曲線関数
2.22 逆双曲線関数
2.23 演習～初等関数
2.24 関数の極限
2.25 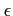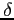$\epsilon$ - $\delta$ 論法
2.26 関数の極限の性質
2.27 関数の極限の確定と不確定
2.28 代入だけの極限の計算
2.29 有理式の極限の計算
2.30 関数の収束の速さを比較して極限の計算
2.31 はさみうちの定理による極限の計算
2.32 根号の有理化による極限の計算
2.33 変数をおきかえて極限の計算
2.34 自然対数の底の公式を用いた極限の計算
2.35 sinc 関数を用いた極限の計算
2.36 双曲線関数の極限の計算
2.37 連続と不連続
2.38 みかけ上の不連続点
2.39 連続関数
2.40 演習～極限，連続

平成22年6月17日